Determination of Breakthrough Curves and Effective Gas Sorption Capacities

Introduction

Dynamic breakthrough experiments provide a powerful tool to assess the effective sorption capacity of porous materials exposed to flowing gas mixtures. In a typical breakthrough experiment, a flowing gas containing a well-defined concentration of adsorptive in a carrier gas passes through an adsorber column containing a porous sample. After some time, the adsorbent becomes saturated with adsorbed gas. From that point on, no additional gas can be adsorbed, and further adsorptive gas entering the column simply travels through to the end of the adsorber column. This transition is commonly referred to as the point at which “the gas breaks through”. Such gas adsorption breakthrough (BT) curves show, in practice, how much gas can be adsorbed by a porous material from a gas flow containing other gas components. A newly developed and fully automatic gas sorption analyzer, the mixSorb L from 3P INSTRUMENTS is a sophisticated analyzer that effectively closes the knowledge gap between equilibrium BET and pore size measurements of porous materials and the dynamic determination of their effective sorption capacities.

Figure 1. Automated analyzer mixSorb L for the determination of breakthrough curves of adsorbents.

Experimental

In a representative example, the sorption column of the mixSorb L was filled with activated carbon (NORIT), purged with nitrogen at 0.5 L/min, and heated at 5 K/min up to 120 °C. The temperature was held at 120°C for 3 hours to flush all impurities and any pre-adsorbed moisture off of the sample. The gas flow was then switched to helium, and the column was flushed with helium at 0.5 L/min for 30 minutes as the system was cooled to 25 °C. The dry sample mass of 51.741 g was determined by use of a balance after the experiment was completed.
To determine the subsequent breakthrough curve, a measurement was performed with a flow of 5 % CO₂ in a carrier gas of helium at 8 bar and 25 °C, using a high precision integrated thermal conductivity detector (TCD) to systematically monitor changes in the concentration of gas exiting the column as a function of time. The breakthrough measurement was defined as a function of the TCD signal from the starting point up to 98 % of the initial CO₂ concentration.

dynaSorb BT: Breakthrough curve (black points) of 5 % CO2 in helium

Figure 2. Breakthrough curve (black points) of 5 % CO₂ in helium on activated carbon (NORIT) at 8 bar and 25°C and the integrated area (green) used to calculate the adsorption capacity on this material.

Results

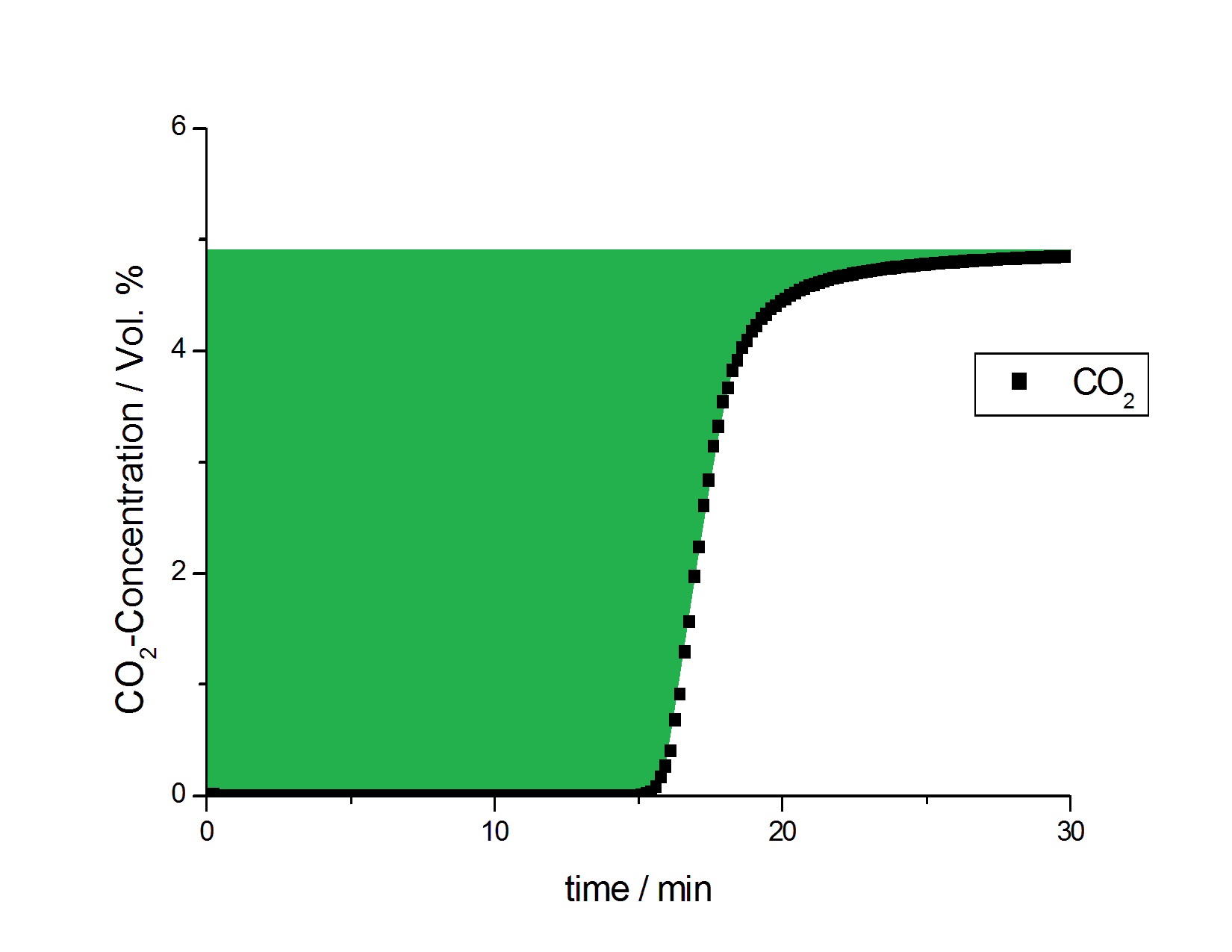
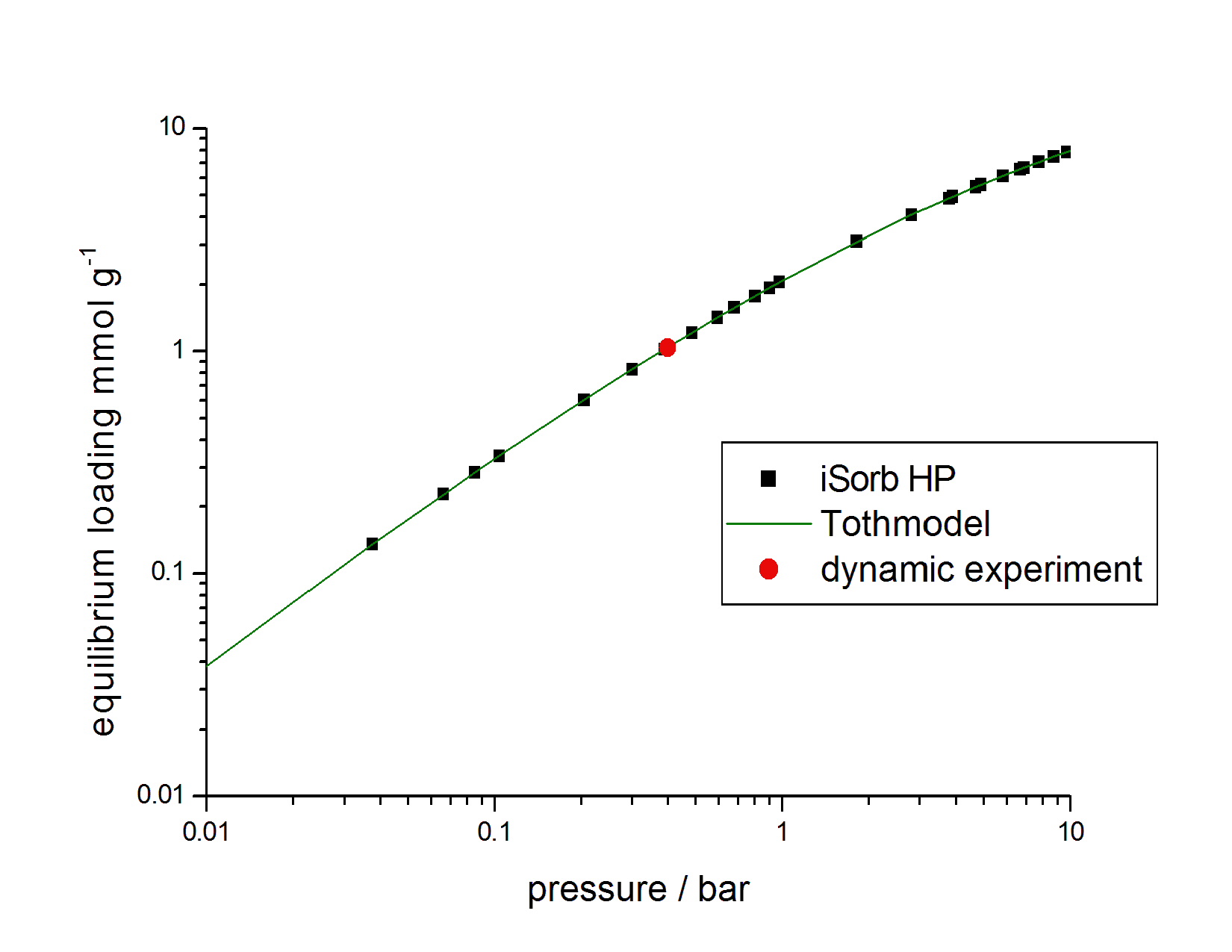
The resulting CO₂ breakthrough curve, illustrating a typical BT curve shape, is shown in Figure 2. The equilibrium loading for the NORIT activated carbon was calculated to be 1.037 mmol/g CO₂ (45.64 mg/g or 23.24 cc/g). This result was compared with static-volumetric isotherm data to check the performance of the mixSorb L instrument. To facilitate this comparison, the concentration of CO₂ was converted to the partial pressure of CO₂ in the gas mixture (the partial pressure of 5 % CO₂ in He at a total pressure of 8 bar being 0.4 bar). Figure 3 shows the dynamic sorption uptake measured on the mixSorb L in comparison to the isotherm of the sample and the Tóth model theory [1]. This illustrates how the measurement results obtained using the mixSorb L are in excellent agreement with the results of the isotherm and with the sorption uptakes predicted using the Tóth model [1].

Although an agreement with the results of other methods is important for validation, it does not fully illustrate the advantages
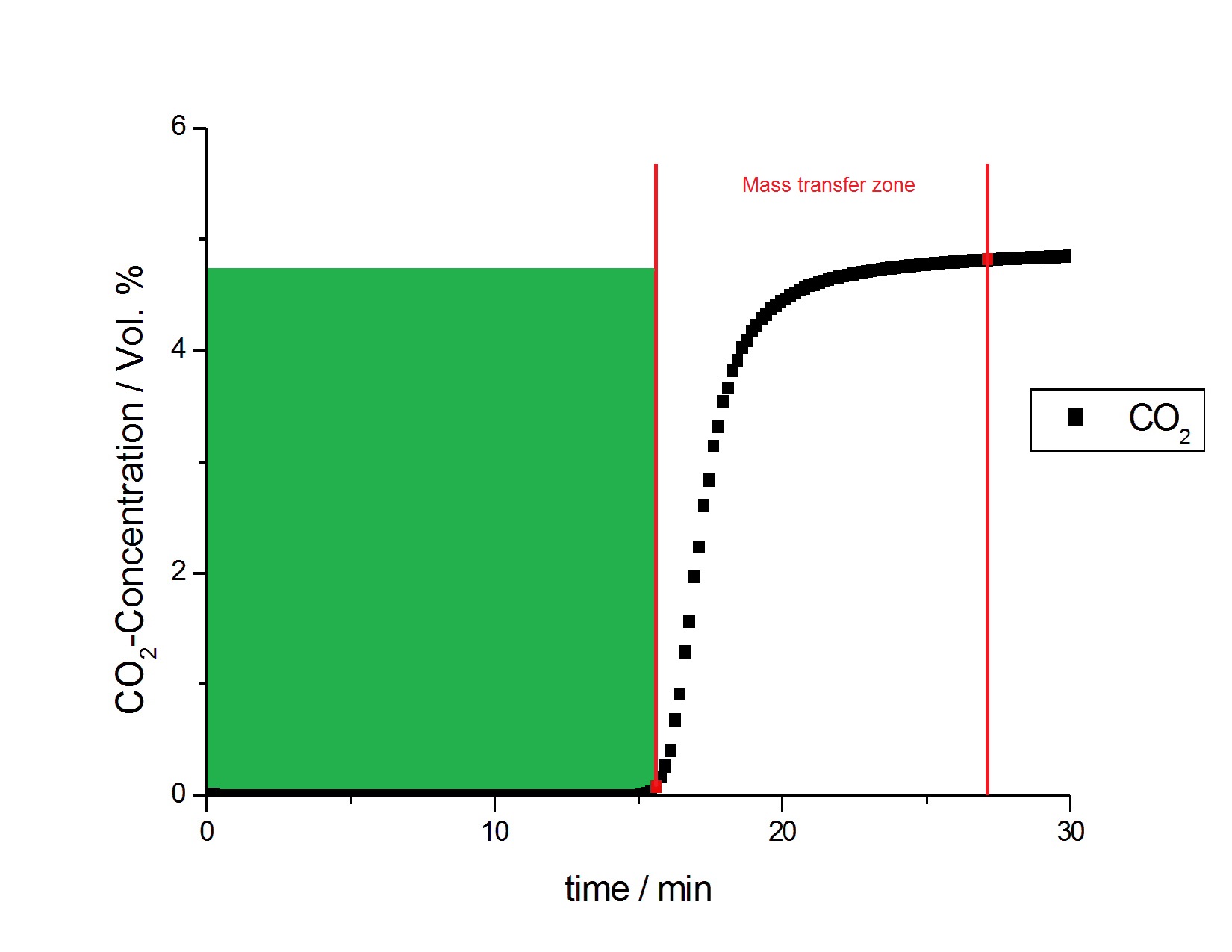
of a new method with a new analytical instrument. The practical importance of the new mixSorb L is that it closes a fundamental gap in knowledge between static equilibrium BET and pore size measurements of porous materials and the determination of their effective sorption capacities under the dynamic conditions that are often found in industrial practice. This is more clearly illustrated in Figure 4, which separates the overall breakthrough curve into two of its main contributors. As seen in Figure 4, the green area now contains only the area below the breakthrough of 0.1 % CO₂. In the case of an application where the breakthrough of one gas component should be prevented, the effective adsorption capacity will be smaller compared to the equilibrium gas capacity calculated from Figure 2.

In the experiment, the effective adsorption capacity of the activated carbon before breakthrough of 0.1 % CO₂ was 0.941mmol/g; this is 90.7 % of the 1.037 mmol/g equilibrium capacity found from Figure 2.

Comparison of sorption capacities determined using a volumetric method (iSorb-HP, Quantachrome), theoretical calculations and a dynamic breakthrough experiment for CO2 on activated carbon at 25 °C (dynaSorb BT, Quantachrome)

Figure 3. Comparison of sorption capacities determined using a volumetric method, theoretical calculations (Tóth model [1]), and a dynamic breakthrough experiment for CO2 on activated carbon at 25 °C (mixSorb L, 3P INSTRUMENTS).

Breakthrough curve (black points) of 5 % CO2 in He on activated carbon (NORIT) at 8 bar and 25 °C; the integrated area (green) is now the area before the breakthrough of 0.1 % CO2

Figure 4. Breakthrough curve (black points) of 5 % CO₂ in He on activated carbon (NORIT) at 8 bar and 25 °C; the integrated area (green) is now the area before the breakthrough of 0.1 % CO₂. The mass transfer zone illustrates the difference between equilibrium adsorption capacity and effective adsorption capacity on this material.

Conclusion

How does one measure the effective adsorption capacity of a porous material related to a gas X, at temperature Y, and some other conditions Z? The breakthrough experiment described in this Note shows that the effective adsorption capacity of the sample studied is only 90.7 % of the equilibrium capacity. The equilibrium adsorption capacity can be estimated by various methods; however, neither a standard BET surface area determination or full isotherm collection for pore size measurement, nor other equilibrium volumetric or gravimetric analyses, can answer the question about the effective adsorption capacity of an adsorbent X, at temperature Y, and other conditions Z.
Only by use of the dynamic method to measure breakthrough curves is one able to determine such effective sorption capacities, which provide the necessary information for the assessment of gas separation processes. Now such valuable performance properties of porous materials for specific gas separation applications can be derived from dynamic breakthrough experiments in lab scale with the fully automated dynamic gas sorption analyzer mixSorb L.

Reference

[1] J. Tóth, Adv. Colloid. Interf. Sci. 55, 1-239 (1995).

Download this Application Note

Back to Resources